Cosine similarity in search engine optimization

What is cosine similarity?

This is the cosine measurement of an angle between non-zero vectors to determine how closely similar they are i.e vector A and vector B having an angle $\theta$ between them, the cosine similarity will be the $\cos \left(\theta \right)$.

The mathematical formula

$\cos \left(\theta \right)=\frac{A\cdot B}{\parallel A\parallel \cdot \parallel B\parallel }$

Where $A\cdot B$ is the dot product of the two vectors and $\parallel A\parallel \cdot \parallel B\parallel$ is the product of the length or magnitude of vector A and vector B.

Example: We find the cosine similarity of two-dimensional vectors A and B in the diagram below.

$\cos \left(\theta \right)=\frac{A\cdot B}{\parallel A\parallel \cdot \parallel B\parallel }$

$A\cdot B=3*4\; +\; 4*2\; =\; 20$

$\parallel A\parallel \cdot \parallel B\parallel =\sqrt{25}*\sqrt{20}=10\sqrt{5}$

$\cos \left(\theta \right)=0.8944$

The measurement always arranges from -1 to 1, where 1 shows that the vectors are similar while the -1 shows that the vectors are opposite of each other or totally dissimilar.

So when it comes to words, a cosine similarity of 0.5 indicates a moderate level of similarity between words, meaning they share some common features or terms but are not identical.

Cosine similarity significance in SEO

Implementing this simple algebra during your keyword research analysis can help by giving you closely related words, which you can use to get your page ranked for the same search intent instead of choosing from a broad list of keywords.

Practical use of cosine similarity

Apart from keyword research analysis, cosine similarity is useful in the following SEO tasks:

1. Comparing your page with competitors’ pages – For this, consider both the term frequency-inverse document frequency (TF-IDF) and cosine similarity to see how important terms are on their pages and how similar they are to your page.
2. SERPs analysis - Using queries from Google search console(GSC) that gives you impressions, you can compare how search engines consider those queries similarity to your page and to pages ranking higher than you. The results will give you a hint to improve your content quality or work on authority.
3. Avoiding keyword cannibalization – Identify which pages within your website compete for the same keyword and might confuse search engines.
4. Interlinking decisions – Helps structure the site more effectively.

Search engines use of numerical vectors

Search engines are machines that work primarily with numbers to understand the semantic meaning of text. By finding words or phrases with the highest cosine similarity, you can optimize your page to rank for all queries related to those words.

Converting text to vectors

Phrases can be converted to vectors by counting word occurrences. For example, for the keywords “SEO services” and “SEO audit,” you can create a vocabulary {SEO, services, audit} after tokenization.

To get the similarity of two phrases: “SEO services” → vector [1, 1, 0] “SEO audit” → vector [1, 0, 1]

$\cos \left(\theta \right)=\frac{A\cdot B}{\parallel A\parallel \cdot \parallel B\parallel }$

$A\cdot B=1*1\; +\; 1*0\; +\; 0*1\; =\; 1$

$\parallel A\parallel \cdot \parallel B\parallel =\sqrt{2}*\sqrt{2}=2$

$\cos \left(\theta \right)=\frac{1}{2}=0.5$

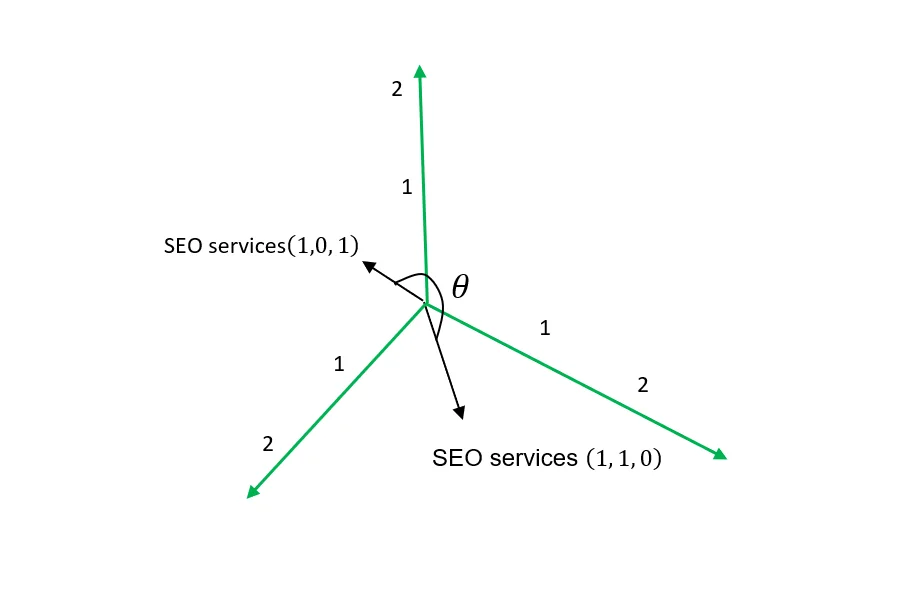
Doing the math above manually would be hectic or nearly impossible in real-world scenarios with high-dimensional vector spaces.

The manual math is also weak for short keywords because it ignores important factors such as weighting of words and subword relationship. This is where word embedding comes in.

Word embedding is the computational implementation of the distributional hypothesis, where computers use natural language processing (NLP) to convert words in a corpus into numerical vectors to understand their semantic meaning and relationships.

There are many tools and libraries for word embedding, such as Word2Vec, developed by Google researchers. Word2Vec uses a continuous bag-of-words (CBOW) and skip-gram approach to learn static word representations based on context.

Implementing this technique is practical because Google has been using it for ranking pages on their search engine.

Implementing word embedding

I have tried using both Word2Vec and Transformer-based embedding models, but I eventually settled on the Transformer-based approach because I had access to a pretrained transformer model all-MiniLM-L6-v2 that encodes phrases efficiently.

So, how do you get the generated word embeddings?

For example, suppose I want to extract keywords from competitors in Kenya who offer SEO services, determine the similarities between these keywords, and use them to optimize my page.

To save time and effort, I have already written a Python script using a Transformer-based embedding model.

Script to generate keyword embeddings

The script extracts keywords from competitor websites, generates embeddings using a Transformer-based model, and calculates cosine similarity between the keywords.

import requests
import re
import nltk
import pandas as pd
from bs4 import BeautifulSoup
from nltk.util import ngrams
from collections import Counter
from sentence_transformers import SentenceTransformer, util
nltk.download("punkt")
urls = {
    "competitor_1": "https://kenseo.co.ke/",
    "competitor_2": "https://artlydigitalmarketing.co.ke/top-seo-agency-in-kenya/",
    "competitor_3": "https://www.seosmart.co.ke/",
}
MIN_PHRASE_FREQ = 2
MIN_PHRASE_LEN = 12
NGRAM_RANGE = (2, 4)
def fetch_clean_text(url):
    headers = {"User-Agent": "Mozilla/5.0"}
    html = requests.get(url, headers=headers, timeout=15).text
    soup = BeautifulSoup(html, "lxml")
    for tag in soup(["script", "style", "nav", "footer", "header", "noscript"]):
        tag.decompose()
    text = soup.get_text(separator=" ")
    text = re.sub(r"\s+", " ", text)
    return text.lower()
def extract_phrases(text, min_n=2, max_n=4):
    tokens = re.findall(r"[a-zA-Z]+", text)
    phrases = []
    for n in range(min_n, max_n + 1):
        phrases.extend([" ".join(g) for g in ngrams(tokens, n)])
    return phrases
all_phrases = []
for name, url in urls.items():
    text = fetch_clean_text(url)
    phrases = extract_phrases(text, *NGRAM_RANGE)
    all_phrases.extend(phrases)
    print(f"Processed: {name}")
phrase_counts = Counter(all_phrases)
keywords = [
    phrase for phrase, count in phrase_counts.items()
    if count >= MIN_PHRASE_FREQ and len(phrase) >= MIN_PHRASE_LEN
]
model = SentenceTransformer("all-MiniLM-L6-v2")
embeddings = model.encode(keywords, convert_to_tensor=True)
cosine_matrix = util.cos_sim(embeddings, embeddings)
similarity_df = pd.DataFrame(
    cosine_matrix.cpu().numpy(),
    index=keywords,
    columns=keywords
)
similarity_df.to_excel("competitor_keyword_similarity2.xlsx")

  

Keyword analysis using cosine similarity

So what I basically always do is search for something in my niche, such as “SEO services in Kenya”, on Google and get the top-ranking websites for this phrase. I then collect the exact URLs that were ranked, maybe the top 5 or 10, because that is where you want to be.

You can also use other tools such as Semrush to get these URLs, but having your primary data is always better.

With the URLs available, just import them into the script and generate a full list of keywords with the cosine similarity calculated between each other.

Your job now is only to sort the ones that have high cosine similarity and use them to optimize your page.

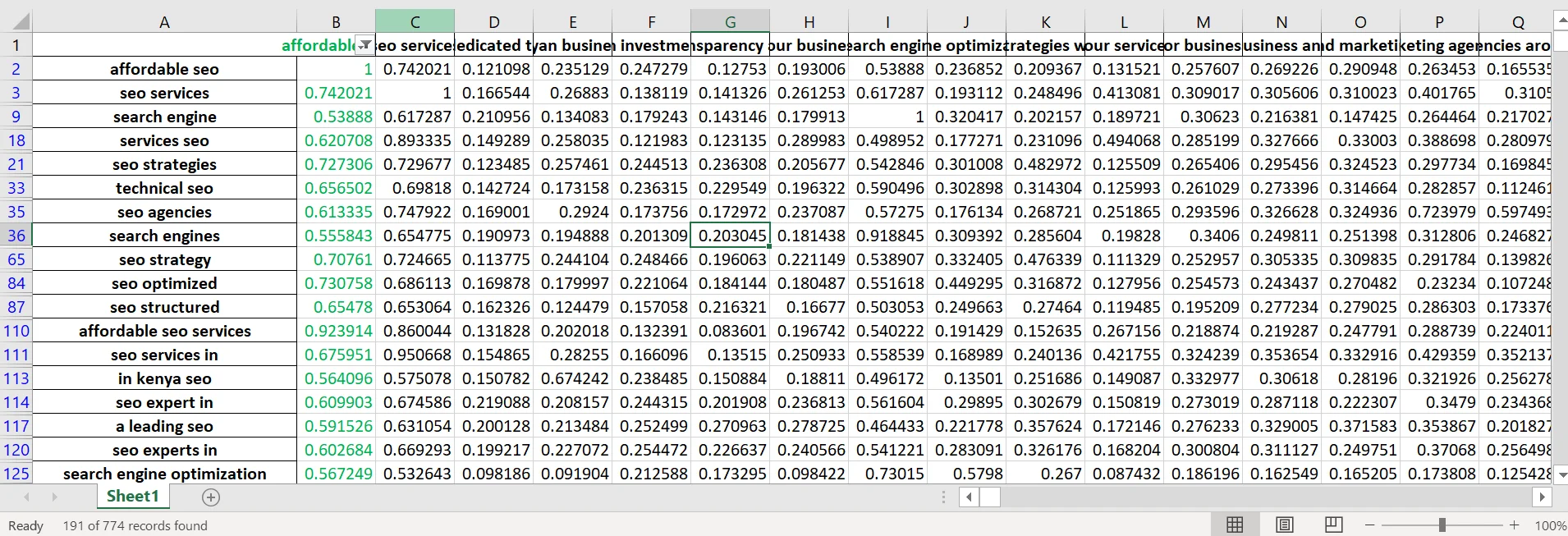
For example, I got 774 keywords from three competitors, and when I chose the one I thought was relevant to my page, i.e., “affordable SEO,” and filtered with the criteria of related keywords having a cosine similarity greater than or equal to 0.5, I ended up with just 191 words that I can use on the same page.

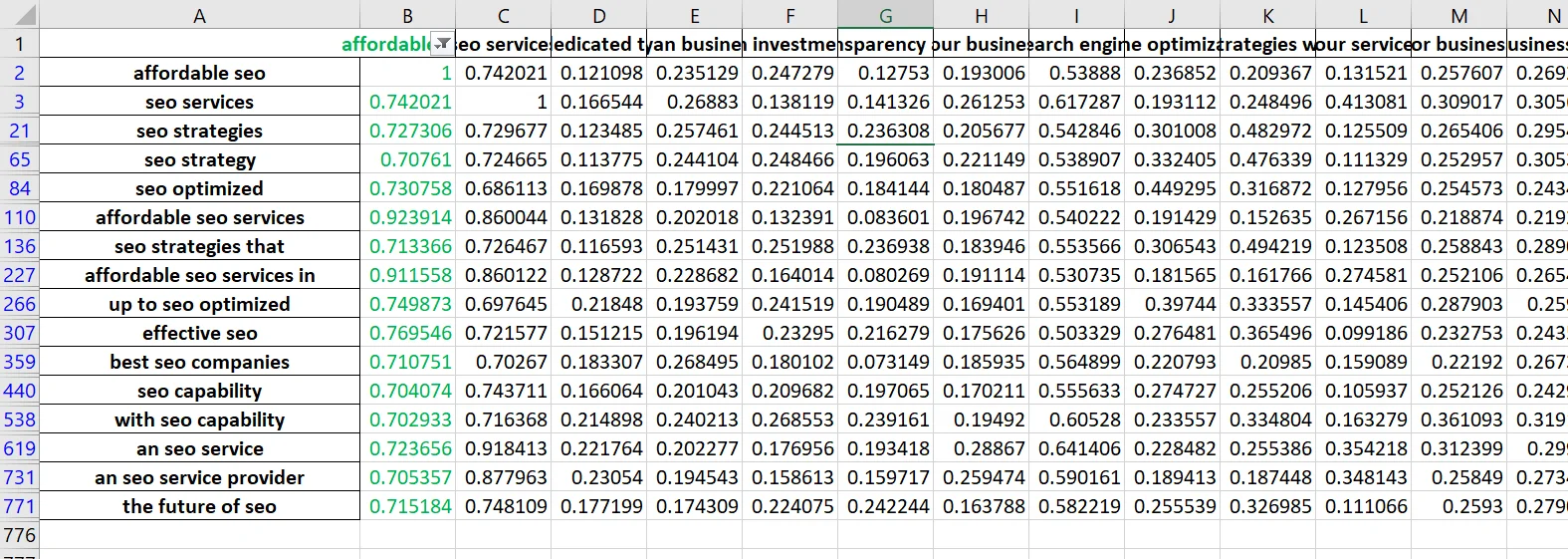
I can reset my filter criteria and get only those that are much closely related e.g greater or equal to 0.7 cosine similarity and have 16 keywords that will have similar search intent ranking.

Hopefully I am not the one finding this interesting as a math nerd, I hope you find it helpful and time saving as well cheer!